Poster zum download als pdf (A4, ca. 4,1 MB)

Poster zum download als pdf (A2, ca. 28,5 MB)

Eine doppeltperiodische Minimalfläche. Stimuliert durch die Entdeckung der Costafläche wurden seit 1980 viele weitere eingebettete Minimalflächen gefunden. Die hier dargestellte gehört zu den einfachsten. Sie wird doppeltperiodisch genannt, weil sich ihr Bild nach oben und nach rechts hinten periodisch wiederholt. Nach beiden Seiten läuft diese Fläche in parallele Halbebenen aus -- das gezeigte Bild ist allerdings auch mit der Vorstellung verträglich, dass die Fläche sich auch in dieser seitlichen Richtung periodisch wiederholt, also eine dreifach periodische Fläche zu sehen ist. Interpretiert man die Einheitsnormalen der Fläche als Abbildung in die Riemannsche Zahlenkugel, so kann man das Bild als Veranschaulichung einer elliptischen Funktion ansehen. Diese hat auf ihrem Fundamentalbereich zwei einfache Nullstellen und zwei einfache Pole.

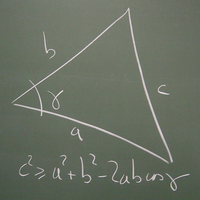Die Geometrie in gekrümmten Räumen unterscheidet sich von der Euklidischen Geometrie. Das Bild zeigt ein Dreieck in einem negativ gekrümmten Raum. Die Ungleichung bringt zum Ausdruck, dass die Seiten von Dreiecken in solchen Räumen länger sind, als wir es von den Winkeln her erwarten würden. Die nichteuklidische Geometrie von Bolyai und Lobatschewski ist das erste Beispiel eines negativ gekrümmten Raumes. Unsere Welt wird in der allgemeinen Relativitätstheorie in einem erweiterten Sinne als gekrümmter Raum betrachtet.

Die am besten bekannten Kleinschen Flaschen sind die seit Ende des 19. Jahrhunderts aus Glas hergestellten Exemplare. Sie sind spiegelsymmetrisch. Die hier dargestellte Kleinsche Flasche ist nicht durch Immersionen in ein spiegelsymmetrisches Exemplar deformierbar. Natürlich dient der Schlitz nur zum Hineinsehen: das dargestellte Stück ist zweiseitig gefärbt und erst, wenn man den Schlitz schließt, entsteht die einseitige (oder nicht orientierbare) Kleinsche Flasche.

Felix Klein wurde 1849 als Sohn eines preußischen Beamten in Düsseldorf geboren. Er studierte in Bonn, vor allem bei Julius Plücker, und promovierte hier im Alter von 19 Jahren. Nach Studienaufenthalten in Göttingen und Berlin wurde er 1872 Ordinarius in Erlangen, ging 1875 an die TH München, 1880 nach Leipzig und 1886 nach Göttingen, wo er 1913 emeritiert wurde. Er starb am 22. Juni 1925 in Göttingen. Klein leistete bedeutende Beiträge zur Geometrie (nichteuklidische Geometrie, Erlanger Programm), Funktionentheorie (Theorie der automorphen Funktionen) und Algebra (Gruppentheorie, Gleichungen 5. Grades). Er war ein einflussreicher akademischer Lehrer und sehr erfolgreicher Lehrbuchautor. Seine Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert sind ein Klassiker der mathematikhistorischen Literatur. Große Verdienste erwarb sich Klein auch als Wissenschaftsorganisator (Enzyklopädie der Mathematischen Wissenschaften, Förderung der angewandten Mathematik) und auf mathematisch-pädagogischem Gebiet (Lehrerfortbildung, Erhöhung der Rolle der Mathematik im gymnasialen Unterricht).

Moleküldynamik Simulation der Rayleigh-Taylor-Instabilität. Die Rayleigh-Taylor-Instabilität ist eine aus der Fluid-Dynamik bekannte physikalische Instabilität, die in vielen Bereichen der Natur zu beobachten ist. Sie entsteht, wenn ein Fluid unter Schwerkrafteinfluss über ein Fluid mit geringerer Dichte geschichtet wird.

Die Extraktion von Bewegungsfeldern aus Videosequenzen stellt ein grundlegendes Problem im Bereich Computer-Vision dar. Die genaue Berechnung von Objektbewegungen aus Bilddaten ist von überragender Bedeutung in der Robotik, der Videoüberwachung und der Quantifizierung von Bewegungs- und Wachstumsprozessen. In einem neuen Ansatz wurden die Aufgabenstellung der Bewegungsextraktion, der Bildentrauschung und der Segmentierung ineinander verschränkt. Die gemeinsame Bearbeitung erlaubt die geschickte Kombination von methodischen Ansätzen. So werden Kantenflächen in Raumzeit extrahiert, Geschwindigkeitsfelder mit Unstetigkeiten an diesen Flächen berechnet und gleichzeitig die Bildsequenz unter einer Kontinuitätsannahme der Bewegung in der Zeit geglättet. In dem Motiv ist farbkodiert das Bewegungsfeld einer Fußgängerszene dargestellt. Deutlich zu erkennen sind die Unstetigkeiten an den Objektkonturen.

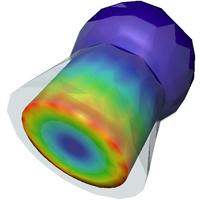Die elastische Deformation eines Korkens in einem Flaschenhals ist charakterisiert durch hohe Spannung im Kontaktbereich, dort wo der Korken der Zwangsbedingung des engen Flaschenhalses ausgesetzt ist. Monotone Mehrgitterverfahren machen es möglich, solche dreidimensionalen Kontaktprobleme mit der gleichen Effizienz zu lösen, wie Probleme ohne Zwangsbedingung. Die Methode erfordert dabei keine Regularisierungstechnik im Hinblick auf die Singularitäten der elastischen Deformation und ermöglicht gerade deshalb eine besonders exakte Berechnung schon bei moderater Feinheit des Rechengitters.

Ostwaldreifung von Tropfen auf dünnen Flüssigkeitsfilmen. Eine Konfiguration von Tropfen auf dünnen Filmen vergröbert sich in der Zeit: Die typische Größe eines Tropfens nimmt zu, während die Anzahl der Tropfen abnimmt und der typische Abstand zwischen den Tropfen wächst. Ein Vergröberungsmechanismus beruht auf dem Massefluss, der im Bild durch die roten Pfeile verdeutlicht wird, von den kleineren in die größeren Tropfen durch den Film. Dieser Prozess ist auch bekannt als Ostwaldreifung. Heuristik (basierend auf asymptotischer Analysis) und numerische Simulationen suggerieren ein statistisch selbstähnliches Verhalten des Systems. Mathematisch rigoros können obere Schranken für die Vergröberungsrate bewiesen werden. Die Methode beruht auf der Gradientenflussstruktur der Filmevolution.

Geboren 1868 in Breslau als Sohn eines gebildeten jüdischen Kaufmanns, wurde Felix Hausdorff nach Promotion und Habilitation in Leipzig dort 1901 außerordentlicher Professor, ging dann 1910 als Extraordinarius nach Bonn, 1913 als Ordinarius nach Greifswald und kam 1921 wieder nach Bonn, wo er 1935 emeritiert wurde. Als Jude vom nationalsozialistischen System zunehmend schikaniert und gedemütigt, nahm er sich am 26. Januar 1942 das Leben, als schließlich die Deportation in ein Konzentrationslager drohte. Hausdorff war ein bedeutender und außerordentlich vielseitiger Mathematiker. Er begründete die allgemeine Topologie als eigenständige mathematische Disziplin und leistete bedeutende Beiträge zur allgemeinen und deskriptiven Mengenlehre, zur Maßtheorie, Algebra, Funktionalanalysis, Wahrscheinlichkeitstheorie und Versicherungsmathematik. Sein klassisches Werk Grundzüge der Mengenlehre (1914) war ein Meilenstein in der Entwicklung der mengentheoretisch-axiomatisch fundierten modernen Mathematik des 20. Jahrhunderts. Hausdorff hat in den Jahren 1897--1912 unter dem Pseudonym Paul Mongré einen Aphorismenband, ein erkenntniskritisches Buch, einen Gedichtband, ein in über 30 Städten Europas mehr als 300 mal aufgeführtes Theaterstück und eine Reihe von Essays in damals renommierten literarischen Zeitschriften publiziert und war als philosophisch-literarischer Schriftsteller in der intellektuellen Sphäre Deutschlands um die Jahrhundertwende eine bemerkenswerte und beachtete Erscheinung.

Numerische Berechnung der Elektronenstruktur einer geschlossenen Bornitrid-Nanoröhre. Bornitrid-Nanoröhren sind durch numerische Berechnungen mit Dichtefunktionalmethoden vorhergesagt und daraufhin synthetisiert worden. Sie haben ähnlich faszinierende Materialeigenschaften, wie die bereits in der Nanotechnologie vielfach verwendeten Kohlenstoff-Nanoröhren.

Der America´s Cup ist über die letzten 150 Jahre hinweg ein herausragendes Erprobungsfeld für Segler und ihre Boote. Um der Beste in diesem Feld zu sein, ist es unerlässlich, auch technologisch höchste Standards zu erreichen und innovativ zu sein. Strömungssimulationen wurden von A. Quarteroni und Mitarbeitern über Jahre hinweg als Werkzeug in der Optimierung von Jachten eingesetzt. Die mathematischen Gleichungen, welche dreidimensionale, inkompressible, turbulente Strömungen beschreiben, sind ein Satz komplizierter gekoppelter partieller Differentialgleichungen. Ihre Diskretisierung erfordert genaue und robuste numerische Methoden und große Rechenleistung. Eine besondere Schwierigkeit im Jachtdesign ist die Komplexität der physikalischen Modellierung im Zusammenhang mit der Kopplung von Wasser- und Luftströmung, Wellenformation an der Wasseroberfläche und Interaktion von Strömung, Segel und Mast.

Parametrisierungen zweidimensionaler Flächen können beschrieben werden als Minima einer geeigneten Energie. Geeignete Maße der Verzerrung durch die Parametrisierung lassen sich auf Axiomen ableiten, ähnlich dem axiomatischen Zugang zu mechanischen Fragestellungen. Die sich ergebenden Modelle sind eng verwandt zur nichtlinearen Elastizitätstheorie. Parametrisierungen lassen sich optimieren in Bezug auf die Bedeutung von Längen- und Flächenerhaltung sowie Winkeltreue. Das Bild zeigt ein mittels Parametrisierung auf die Fläche übertragenes Schachbrettmuster. Die zugrunde liegende diskrete Fläche setzt sich aus ca. 75000 Dreiecken zusammen.

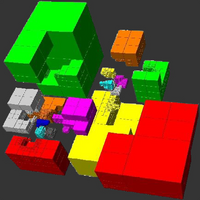Verteilung eines adaptiven dreidimensionalen Diskretisierungsgitters auf mehrere Prozessoren (farblich unterschieden) mittels einer raumfüllenden Kurven-Heuristik. Das Ziel bei der Parallelisierung von Programmen ist es zu erreichen, dass die Prozessoren alle näherungsweise die gleiche Last erhalten, wobei gleichzeitig die Kommunikation zwischen den Prozessoren minimiert wird.

Geometrie und freie Oberflächen-Strömung durch eine Schleuse, das Geschwindigkeitsfeld der Strömung ist farblich kodiert. Bei der Entwicklung und dem Bau von Schleusen ist es besonders wichtig, auf die Strömungsverhältnisse, insbesondere auf die Entstehung von Turbulenzen beim Öffnen und Schließen der Schleuse, zu achten.

Georg Cantor wurde 1845 in Sankt Petersburg als Sohn eines Kaufmanns geboren. Er studierte in Berlin, habilitierte sich in Halle und war dort von 1879 bis zu seiner Emeritierung im Jahre 1913 Ordinarius für Mathematik. Er starb am 6. Januar 1918 in Halle. Ausgehend von Untersuchungen über die Eindeutigkeit der Fourierentwicklung begann Cantor das Studium von Punktmengen. Dies führte ihn zu seiner wichtigsten Leistung, der Theorie der transfiniten Ordinal- und Kardinalzahlen. Cantor wurde damit zur zentralen Figur bei der Herausbildung der Mengenlehre. Während die allgemeine Mengenlehre anfangs wenig beachtet und sogar von bedeutenden Mathematikern zurückgewiesen wurde, wurden Cantors Forschungen über Punktmengen (mengentheoretische Topologie, Theorie von Inhalt und Maß) sofort anerkannt und von anderen Mathematikern aufgenommen und weiterentwickelt. Die Mengenlehre hat das Gesicht der Mathematik einschneidend verändert -- sie war eine der Voraussetzungen für die Entwicklung der modernen Strukturmathematik des 20. Jahrhunderts. Cantor hat wesentlichen Anteil an der Gründung der Deutschen Mathematiker-Vereinigung im Jahre 1890 und war ihr erster Vorsitzender. Er bemühte sich auch intensiv um die Etablierung internationaler Mathematikerkongresse.

Adaptive Rekonstruktion ungeordneter Daten mit Spline-Wavelets - Die numerische Rekonstruktion von Oberflächen auf Basis von großen Datensätzen über irregulären Punktmengen führt bei Verwendung uniformer Diskretisierungen zu sehr hohen Kosten. Diese lassen sich massiv verringern durch geeignete adaptive Methoden, die sich automatisch der Auflösung und Struktur der Daten anpassen. Hierfür setzen wir Spline-Wavelets ein, die als lokale Basisfunktionen von uniformer Kondition die Lösung der entstehenden linearen Gleichungssysteme in optimaler linearer Komplexität erlauben. Auch Störungen und Fehler in den Daten können mit diesem Ansatz korrigiert werden. In verschiedenen Projekten werden die vorteilhaften Eigenschaften von Waveletbasen außerdem zur effizienten numerischen Lösung von elliptischen und parabolischen partiellen Differentialgleichungen und von Kontrollproblemen unter PDG-Nebenbedingungen eingesetzt und zur Auflösung von Nichtlinearitäten in Erhaltungsgleichungen.

Ferromagnetische Formgedächtnismaterialien erlauben die Dehnung und Stauchung des Werkstoffs durch Einfluss äußerer Magnetfelder. Für technisch schwierig herzustellende einkristalline Werkstoffe lassen sich Dehnungen von bis zu 10% erreichen. In polykristallinen Materialien geht dieser Effekt ganz wesentlich zurück, da sich die unterschiedlichen Körner des metallischen Materials gegenseitig in der Dehnung behindern. Eine jüngst vorgeschlagene Alternative ist die, einkristalline Formgedächtnispartikel in ein weiches Polymer einzubetten. Die Produktion eines solchen Materials ist viel einfacher und kostengünstiger als die großer Einkristalle. Modellrechnungen bestätigen, dass man mit diesem zusammengesetzten Material sehr gute Dehnungen erwarten darf. Dargestellt sind hier einige solche Partikel in einer deformierten Zelle einer in beiden Richtungen in zwei Dimensionen periodischen Materialstruktur. Farblich kodiert sind die Spannungen im Polymer.

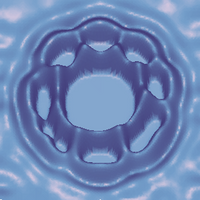Satellitenlöcher - Momentaufnahme eines Entnetzungsprozesses. Das Benetzungsverhalten dünner Flüssigkeitsfilme ist vielgestaltig, und selbst komplexe Vorgänge lassen sich mit der Dünne-Filme-Gleichung, einer degeneriert parabolischen PDG vierter Ordnung, oft überraschend einfach modellieren. Das vorliegende Simulationsbild zeigt eine Momentaufnahme eines kaskadenförmigen Entnetzungsvorgangs. Dabei bilden sich in einem annähernd gleichmäßig dicken Film um eine Anfangsvertiefung herum kaskadenartig Ringe mit Satellitenlöchern - ein Phänomen, das experimentell z.B. bei der Entnetzung von Polystyrol-Filmen auf Silizium-Oxid-Substrat beobachtet wird. Aus einer Musteranalyse mit Minkowski-Funktionalen geht hervor, dass sich die Filmmorphologien in physikalischem Experiment und dimensionsbehafteter numerischer Simulation durch das gleiche Gauß'sche Wahrscheinlichkeitsfeld beschreiben lassen.

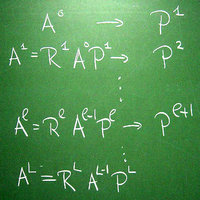Konstruktion einer Hierarchie von Matrizen für ein algebraisches Mehrgitterverfahren. Mehrgitterverfahren sind numerische Methoden zur Lösung großer, schwach besetzter linearer Gleichungssysteme in linearer Zeit. Algebraische Mehrgitterverfahren konstruieren die dafür benötigte Hierarchie von Gittern und Matrizen automatisch anhand des ursprünglichen linearen Gleichungssystems.

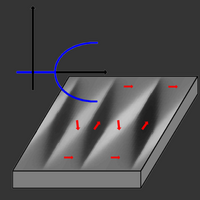Das Bild zeigt das so genannte Konzertinamuster. Dabei handelt es sich um einen Zustand der Magnetisierung im mehrskaligen mikromagnetischen Modell. Das Muster geht aus einem uniformen Grundzustand durch eine Bifurkation in einem speziellen Parameterbereich hervor. Die Bifurkation wird durch Anlegen eines äußeren Feldes in Gegenrichtung zum Grundzustand hervorgerufen. Das Konzertinamuster zeichnet sich durch eine intrinsische Periodizität aus, die sich in den übrigen drei Parameterbereichen nicht zeigt.